刚开始Fei Fei教授介绍了计算机视觉发展史，比如自己团队搭建的imagenet数据集，从10亿张图片中清洗出1500万张图片，然后标注出22000个类（个人认为这个数据集是人工智能能走出寒冬的根本原因，因为他太庞大了，数据才是模型的关键驱动），并基于此开展了一个图像分类的比赛，在2012年一个叫AlexNet的模型脱颖而出，发明这个模型的人就是我们现在熟知的Geoffrey Hinton，这就是现代人工智能和现代深度学习的开端，从那以后，深度学习迅猛发展，人工智能成为时代新浪潮。

图像分类（classification）

许多看似不同的计算机视觉任务（例如目标检测、图像分割）都可以归结为图像分类问题。 对于计算机而言，图像被表示为一个大型的三维数字数组。例如，一张猫的图像宽 248 像素，高 400 像素，并具有红、绿、蓝三个颜色通道（简称 RGB）。因此，该图像由 248 x 400 x 3 个数字组成，总共 297,600 个数字。每个数字都是一个介于 0（黑色）到 255（白色）之间的整数。我们的任务是将这二十五万个数字转换为一个标签，例如 “猫” 。
如果直接进行硬编码那几乎是不可能的，所以这里我们采用数据驱动方法，比如一个孩子是怎么知道这个东西是一只猫的呢，那是因为他见过大量的猫，以及有人告诉他这就是猫，然后他就会知道哦原来长成这个样的就是猫，训练识别猫的模型的数据驱动方法的原理和这个差不多。

大致流程如下：（比较容易理解）
输入： 我们的输入包含 N 张图像，每张图像都被标记为 K 个不同类别之一。我们将此数据称为训练集 。
学习： 我们的任务是利用训练集来学习每个类别的特征。我们将这一步骤称为训练分类器 ，或学习模型 。
评估： 最后，我们通过让分类器预测一组它从未见过的新图像的标签来评估其质量。然后，我们将这些图像的真实标签与分类器预测的标签进行比较。直观地说，我们希望大部分预测结果与真实答案（我们称之为 “真值 ”）相符。

最近邻分类器

这里对图像的差异用的是L1距离
$$
d_1 (I_1, I_2) = \sum_{p} \left| I^p_1 - I^p_2 \right|
$$
看一张图片就懂了

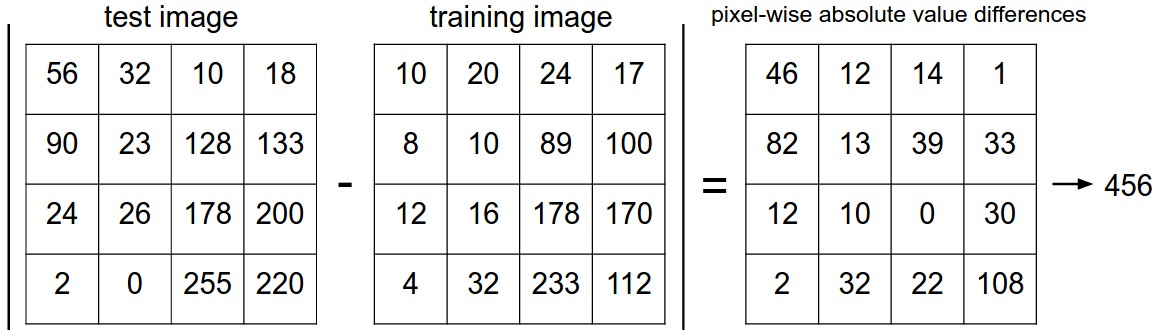
直接看代码
首先，我们将 CIFAR-10 数据集加载到内存中，并将其拆分为 4 个数组：训练数据/标签、测试数据/标签。在下面的代码中， Xtr （大小为 50,000 x 32 x 32 x 3）存储了训练集中的所有图像，而对应的 1 维数组 Ytr （长度为 50,000）则存储了训练标签（从 0 到 9）：

Xtr, Ytr, Xte, Yte = load_CIFAR10('data/cifar10/') # a magic function we provide
# flatten out all images to be one-dimensional
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) # Xtr_rows becomes 50000 x 3072
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3) # Xte_rows becomes 10000 x 3072

现在我们已经将所有图像拉伸成行，接下来我们将介绍如何训练和评估分类器：

nn = NearestNeighbor() # create a Nearest Neighbor classifier class
nn.train(Xtr_rows, Ytr) # train the classifier on the training images and labels
Yte_predict = nn.predict(Xte_rows) # predict labels on the test images
# and now print the classification accuracy, which is the average number
# of examples that are correctly predicted (i.e. label matches)
print 'accuracy: %f' % ( np.mean(Yte_predict == Yte) )

接下来最核心的部分——实际的分类器本身。以下是一个使用 L1 距离的简单最近邻分类器的实现，它满足此模板：

import numpy as np

class NearestNeighbor(object):
  def __init__(self):
    pass

  def train(self, X, y):
    """ X is N x D where each row is an example. Y is 1-dimension of size N """
    # the nearest neighbor classifier simply remembers all the training data
    self.Xtr = X
    self.ytr = y

  def predict(self, X):
    """ X is N x D where each row is an example we wish to predict label for """
    num_test = X.shape[0]
    # lets make sure that the output type matches the input type
    Ypred = np.zeros(num_test, dtype = self.ytr.dtype)

    # loop over all test rows
    for i in range(num_test):
      # find the nearest training image to the i'th test image
      # using the L1 distance (sum of absolute value differences)
      distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
      min_index = np.argmin(distances) # get the index with smallest distance
      Ypred[i] = self.ytr[min_index] # predict the label of the nearest example

    return Ypred

当然也可以使用L2距离
$$
d_2 (I_1, I_2) = \sqrt{\sum_{p} \left( I^p_1 - I^p_2 \right)^2}
$$
只需要替换一行代码

distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))

k-最近邻分类器

其思想非常简单：我们不是在训练集中找到单个最近邻图像，而是找到最接近的 k 个图像，并让它们对测试图像的标签进行投票。特别地，当 k = 1 时，我们就得到了最近邻分类器。直观地说， k 值越大，分类器对异常值的鲁棒性就越强，从而具有平滑效应。
彩色区域显示了分类器基于 L2 距离生成的决策边界 。白色区域显示了分类模糊的点（即至少两个类别的投票结果相同）。请注意，对于最近邻分类器，异常数据点（例如，位于蓝色点云中间的绿色点）会形成一些可能存在错误预测的小区域，而五近邻分类器可以平滑这些异常值，从而可能在测试数据上获得更好的泛化能力。

k 近邻分类器需要设置 k 值 。但哪个 k 值效果最佳呢？此外，我们还发现可以使用许多不同的距离函数：L1 范数、L2 范数，以及许多其他我们甚至没有考虑过的选择（例如点积）,这些选择被称为超参数。 有一种合适的方法来调整超参数，而且完全不需要修改测试集。其思路是将训练集分成两部分：一个稍小的训练集，以及我们称之为验证集的验证集。

交叉验证

常见的数据划分方法。给定一个训练集和一个测试集。训练集被分成若干折（例如，这里是 5 折）。第 1 到 4 折构成训练集。其中一折（例如，这里黄色的第 5 折）被指定为验证集，用于调整超参数。交叉验证更进一步，它会迭代地选择验证集，与第 1 到 5 折分开进行。这被称为 5 折交叉验证。最后，一旦模型训练完成并确定了所有最佳超参数，模型就会在测试数据（红色）上进行一次评估。

线性分类

线性分类器：
$$
f(x_i, W, b) = W x_i + b
$$
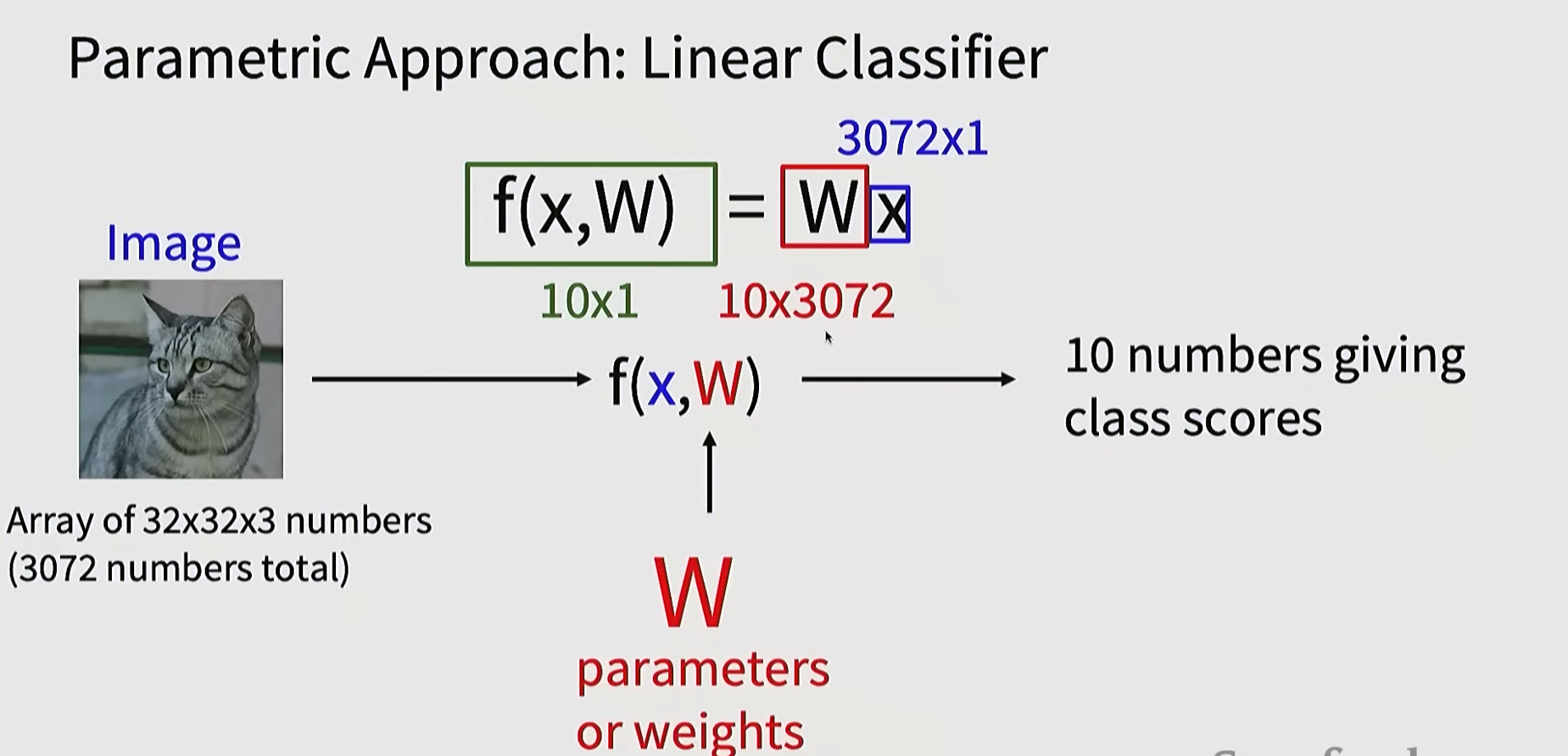
在上述等式中，我们假设图像 (x_i) 的所有像素都被展平为一个形状为 [D x 1] 的单列向量。矩阵 W （大小为 [K x D]）和向量 b （大小为 [K x 1]）是该函数的参数 。在 CIFAR-10 数据集中，(x_i) 包含第 i 幅图像中所有被展平为 [3072 x 1] 列的像素， W 为 [10 x 3072]， b 为 [10 x 1]，因此函数接收 3072 个数字（原始像素值），输出 10 个数字（类别得分）。W 中的参数通常被称为权重 ，而 b 被称为偏置向量， 因为它会影响输出得分，但不直接作用于实际数据 (x_i)。然而，人们经常会交替使用“ 权重” 和 “参数” 这两个术语。

有几点需要注意：
首先，请注意，单个矩阵乘法 (W x_i) 实际上是并行评估 10 个独立的分类器（每个类别一个），其中每个分类器是 W 的一行。
还要注意的是，我们将输入数据 ( (x_i, y_i) ) 视为给定且固定的，但我们可以控制参数 W 和 b 的设置。我们的目标是设置这些参数，使得计算出的分数与整个训练集的真实标签相匹配。我们将更详细地介绍如何实现这一点，但直观地说，我们希望正确类别的分数高于错误类别的分数。
这种方法的优势在于，训练数据用于学习参数 W 和 b ，但一旦学习完成，我们就可以丢弃整个训练集，只保留学习到的参数。这是因为新的测试图像可以简单地输入到该函数中，并根据计算出的分数进行分类。
最后需要注意的是，对测试图像进行分类只涉及一次矩阵乘法和加法运算，这比将测试图像与所有训练图像进行比较要快得多。

下面介绍两种最常见的损失函数

多类支持向量机（SVM）损失

定义损失函数细节的方法有很多种。首先，我们将介绍一种常用的损失函数—— 多类支持向量机 （SVM）损失。SVM 损失的设定是：对于每张图像，SVM“希望”其正确类别的得分比错误类别的得分高出一个固定的间隔 (\Delta)。需要注意的是，像我们上面那样将损失函数拟人化有时很有帮助：SVM“希望”得到某个特定的结果，这个结果能够降低损失（这是好事）。

现在让我们更精确地描述一下。回想一下，对于第 i 个样本，我们给定图像的像素 ( x_i ) 和标签 ( y_i )，该标签指定了正确类别的索引。得分函数接收这些像素，并计算类别得分向量 ( f(x_i, W) )，我们将其简写为 (s)（scores 的缩写）。例如，第 j 个类别的得分是第 j 个元素：( s_j = f(x_i, W)_j )。那么，第 i 个样本的多类 SVM 损失可以形式化地表示如下：

$$
L_i = \sum_{j\neq y_i} \max(0, s_j - s_{y_i} + \Delta)
$$

让我们通过一个例子来解释它是如何运作的。假设我们有三个类别，它们的得分分别为 ( s = [13, -7, 11])，并且第一个类别是正确的类别（即 (y_i = 0)）。同时假设 (\Delta)（一个我们稍后会详细介绍的超参数）为 10。上面的表达式是对所有错误类别（(j \neq y_i)）求和，因此我们得到两项：
$$
L_i = \max(0, -7 - 13 + 10) + \max(0, 11 - 13 + 10)
$$
你可以看到，第一项的结果为零，因为 [-7 - 13 + 10] 是一个负数，所以会被 (max(0,-)) 函数截断为零。对于这一对样本，损失为零，是因为正确类别的得分 (13) 比错误类别的得分 (-7) 至少高出 10 个单位的间隔。实际上，差值为 20，远大于 10，但 SVM 只关心差值是否至少为 10；任何超过间隔的额外差值都会被 max 操作截断为零。第二项计算 [11 - 13 + 10]，结果为 8。也就是说，即使正确类别的得分高于错误类别 (13 > 11)，但差值并没有达到所需的 10 个单位间隔。差值只有 2，这就是为什么损失值为 8（即差值需要高出多少才能满足间隔要求）。总而言之，SVM 损失函数要求正确类别的得分(y_i)至少比错误类别的得分大(\Delta) (delta)。如果达不到这个条件，就会累积损失。

多类支持向量机“希望”正确类别的得分比其他所有类别的得分至少高出一个增量（delta）。如果任何类别的得分位于红色区域内（或更高），则会产生累积损失。否则，损失为零。我们的目标是找到一组权重，使训练数据中的所有样本同时满足此约束，并使总损失尽可能低。

Softmax分类器

事实证明，支持向量机 (SVM) 是两种常见的分类器之一。另一种常用的分类器是 Softmax 分类器 ，它的损失函数与 SVM 不同。与 SVM 将输出 (f(x_i,W)) 视为每个类别的（未经校准且可能难以解释的）分数不同，Softmax 分类器给出了一个更直观的输出（归一化的类别概率），并且还具有概率解释。
Softmax 分类器为每个类别提供“概率”。 与 SVM 不同，SVM 会计算所有类别的未经校准且难以解释的分数，而 Softmax 分类器允许我们计算所有标签的“概率”。例如，给定一张图像，SVM 分类器可能会给出“猫”、“狗”和“船”这三个类别的分数 [12.5, 0.6, -23.0]。而 Softmax 分类器则可以计算这三个标签的概率 [0.9, 0.09, 0.01]，从而可以解释它对每个类别的置信度。然而，我们之所以给“概率”一词加上引号，是因为这些概率的峰值或弥散程度直接取决于正则化强度 (\lambda)——这是您作为系统输入控制的参数。例如，假设三个类别的未归一化对数概率为 [1, -2, 0]。那么，softmax 函数将计算：
$$
[1, -2, 0] \rightarrow [e^1, e^{-2}, e^0] = [2.71, 0.14, 1] \rightarrow [0.7, 0.04, 0.26]
$$
在 Softmax 分类器中，映射函数 (f(x_i; W) = W x_i) 保持不变，但我们现在将这些分数解释为每个类别的未归一化的对数概率，并将铰链损失替换为交叉熵损失， 其形式如下：
$$
L_i = -\log\left(\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} }\right) \hspace{0.5in} \text{or equivalently} \hspace{0.5in} L_i = -f_{y_i} + \log\sum_j e^{f_j}
$$
这里我们使用符号 (f_j) 来表示类别得分向量 (f) 的第 j 个元素。

正则化

正则化主要是为了解决过拟合的问题，最后要达到的效果是降低在训练集上的准确率，提升在测试集上以及以后预测的准确率。
我们可以通过扩展损失函数，添加正则化惩罚项 (R(W)) 来实现了这一点。最常用的正则化惩罚项是平方 L2 范数，它通过对所有参数进行逐元素二次惩罚来抑制过大的权重：
$$
R(W) = \sum_k\sum_l W_{k,l}^2
$$
在上面的表达式中，我们对 (W) 的所有平方元素求和。请注意，正则化函数并非数据函数，它仅基于权重。包含正则化惩罚项后，完整的多类支持向量机损失函数得以实现，该损失函数由两部分组成： 数据损失 （即所有样本的平均损失 (L_i)）和正则化损失 。
那么最终总的损失函数可表示为：

最吸引人的特性是，惩罚较大的权重往往能提高泛化能力，因为这意味着任何输入维度本身都无法对得分产生过大的影响。例如，假设我们有一个输入向量 \(x = [1,1,1,1] \) 和两个权重向量 \(w_1 = [1,0,0,0]\)，\(w_2 = [0.25,0.25,0.25,0.25] \)。那么 \(w_1^Tx = w_2^Tx = 1\)，两个权重向量的点积相同，但 \(w_1\) 的 L2 惩罚为 1.0，而 \(w_2\) 的 L2 惩罚仅为 0.25。因此，根据 L2 惩罚，权重向量 \(w_2\) 更优，因为它能实现更低的正则化损失，从根本上来说，也可以理解为权重更加平均，模型**不依赖任何单一输入维度**。直观地说，这是因为 \(w_2\) 中的权重更小且更分散。由于 L2 惩罚项倾向于更小且更分散的权重向量，因此最终的分类器会倾向于对所有输入维度进行少量考虑，而不是对少数几个输入维度进行过强考虑。正如我们将在后面的课程中看到的，这种效应可以提高分类器在测试图像上的泛化性能，并减少过拟合 。

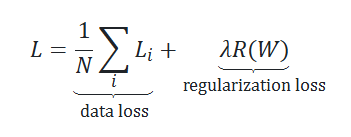
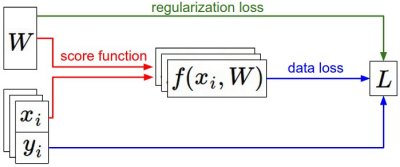
那么接下来，我们要做的就是想办法找到使损失最小的权重。

优化（optimization）

梯度下降方法

我们尝试在权重空间中找到一个方向，以改进我们的权重向量（并降低损失）。结果表明，无需随机搜索一个好的方向：我们可以计算出一个最佳方向，沿着这个方向改变权重向量，该方向在数学上保证是最陡峭的下降方向（至少在步长趋于零的极限情况下如此）。这个方向与损失函数的梯度相关。用徒步旅行来类比，这种方法大致相当于感受脚下山坡的坡度，然后沿着感觉最陡峭的方向向下走，其实本质就是算偏导数。

随机梯度下降（SGD）

我们常常使用小批量梯度下降（随机的选择小批量的样本）：在大规模应用（例如 ILSVRC 挑战赛）中，训练数据可能包含数百万个样本。因此，为了仅进行一次参数更新而计算整个训练集的完整损失函数似乎是一种浪费。解决这一难题的常用方法是计算训练数据批次的梯度。例如，在当前最先进的卷积神经网络中，一个典型的批次包含来自 120 万个样本的整个训练集中的 256 个样本。然后使用该批次进行参数更新：

# Vanilla Minibatch Gradient Descent

while True:
  data_batch = sample_training_data(data, 256) # sample 256 examples
  weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
  weights += - step_size * weights_grad # perform parameter update

SGD + Momentum（动量法）

SGD + Momentum在 SGD 的基础上引入了“速度”的概念，通过累积历史梯度，使参数在一致方向上加速，在震荡方向上减速，可以理解为一个小球从一个坡上滚下来，是带着速度下来的，而不是每一步的速度都重新从0起步，也就是速度是累加的，即梯度是累加的。
$$
v_t = \beta\ v_{t-1} + g_t
$$
$$
w_{t+1} = w_t - \eta\ v_t
$$
一定程度上减少了鞍状底部的影响，使得到达谷底时还能继续往下探索，而不是停在鞍部。

特点：收敛更快，减少梯度震荡。

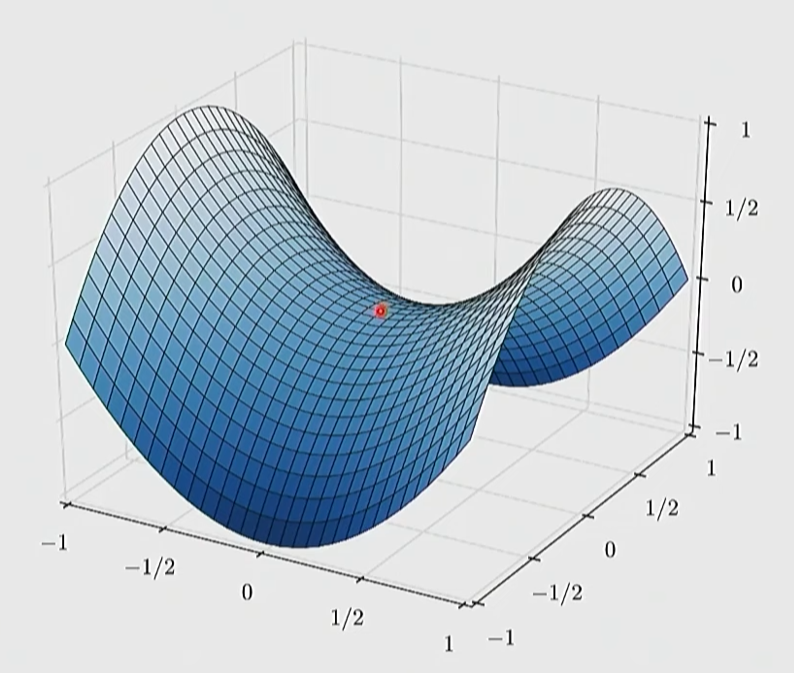
SGD + RMSProp

RMSProp（Root Mean Square Propagation）通过对梯度平方做滑动平均， 为不同参数自动分配不同的学习率（学习率就是η）。
核心思想是：
梯度长期大的方向 → 步子变小
梯度长期小的方向 → 步子变大
$$
s_t = \rho\ s_{t-1} + (1-\rho)\ g_t^2
$$
$$
w_{t+1} = w_t - \eta \ \frac{g_t}{\sqrt{s_t} + \epsilon}
$$
特点：自动调节学习率，也就是自动调整步长。

Adam

Adam将 Momentum（一阶动量） 和 RMSProp（二阶动量） 结合起来，同时解决了梯度方向不稳定和不同参数尺度差异大这两个问题。

一句话总结：
Adam = SGD + Momentum + RMSProp

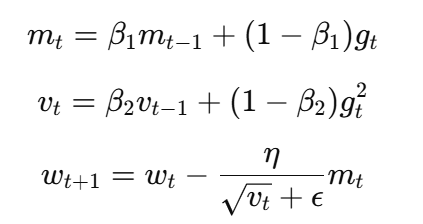
示例代码如下：

特点：收敛快，自动调节学习率，实际工程中最常用。

AdamW(最终版+最优解)

在 Adam 里直接加 L2 正则（把 λw 加到梯度里）并不等价于“真正的权重衰减”，因为 Adam 会用自适应缩放把这个正则项也一起缩放掉，导致“衰减强度”变得不受控。
AdamW 把 权重衰减从梯度里“解耦”出来，单独对参数做衰减。（W指的是Weight Decay，权重衰减）
AdamW 做两件事：
1.用 Adam 正常算梯度更新（只用 ∇L）
2.额外做一次 权重衰减（直接缩小参数）

与传统的Adam+L2不同，AdamW 在计算 L 的梯度时不包含正则项，但在参数更新步骤里单独施加权重衰减，也就是在最后更新参数时进行正则化。

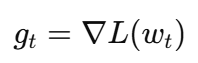
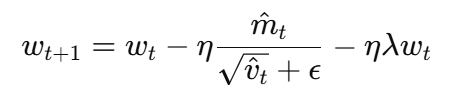
到这里几种基础的分类器以及优化方法就介绍完了，但是最后的分界不可能总是线性的，而且事实证明单独使用这些线性分类器并没有达到我们想达到的效果，因此接下来我们将开始深入学习神经网络和反向传播。